Projeto 1. Simulação de deriva genética.
Utilizando um programa de simulações de Genética de populações, seu grupo deverá simular o processo de deriva genética. Como se trata de um fenômeno em que processos meramente casuais atuam em populações biológicas, não é possível fazer previsões a respeito do resultado em termos de direção (por exemplo, não é possível saber se uma freqüência gênica aumentará ou diminuirá). Entretanto, a magnitude da variação pode ser prevista a partir da variância teórica esperada:
onde d
e2 é a variância esperada, p0 e q0 são as freqüências gênicas iniciais, Np é o tamanho da população e t é o número de gerações.Temos também a equação de estimativa da variância (d
o2, variância observada ou experimental) a partir de dados observados que é:
esta fórmula é algebricamente equivalente a:
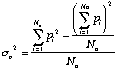
onde p
i é a i-ésima freqüência após t gerações,
é a média das freqüências observadas após t gerações e Na é o número de freqüências abservadas após t gerações.
O objetivo deste projeto é comparar as variâncias observadas e as variâncias teóricas após 15 gerações em populações com tamanhos diferentes: 20, 50, 100, 200 e 500 indivíduos. O programa ilustra graficamente a variação da freqüência de um dos alelos durante todas as gerações, mas os dados a serem utilizados serão apenas os da geração 15. Utilize sempre a mesma freqüência p inicial para todas as simulações (entre 0,33 e 0,66).
A comparação entre as variâncias experimentais e as variâncias teóricas pode ser feita com o teste da razão, onde se estima o parâmetro F que é comparado com o valor crítico:
O F crítico é obtido de uma tabela de valores F críticos, com nível de significância (alfa) de 0,5; bicaudal, com 10 graus de liberdade no numerador e infinitos graus de liberdade no denominador:
|
Tamanho |
freqüências |
obtidas |
p inical= |
|
p 1= |
p 6= |
|
|
|
N=20 |
p 2= |
p 7= |
|
|
p 3= |
p 8= |
|
|
|
F= |
p 4= |
p 9= |
F = |
|
p 5= |
p 10= |
|
|
|
p 1= |
p 6= |
|
|
|
N=50 |
p 2= |
p 7= |
|
|
p 3= |
p 8= |
|
|
|
F= |
p 4= |
p 9= |
F = |
|
p 5= |
p 10= |
|
|
|
p 1= |
p 6= |
|
|
|
N=100 |
p 2= |
p 7= |
|
|
p 3= |
p 8= |
|
|
|
F= |
p 4= |
p 9= |
F = |
|
p 5= |
p 10= |
|
|
|
p 1= |
p 6= |
|
|
|
N=200 |
p 2= |
p 7= |
|
|
p 3= |
p 8= |
|
|
|
F= |
p 4= |
p 9= |
F = |
|
p 5= |
p 10= |
|
|
|
p 1= |
p 6= |
|
|
|
N=500 |
p 2= |
p 7= |
|
|
p 3= |
p 8= |
|
|
|
F= |
p 4= |
p 9= |
F = |
|
p 5= |
p 10= |
|
Com os dados obtidos com o emprego do programa SUPERPOP, preencha a tabela acima e responda:
1. A evolução observada através do processo de deriva genética é também chamada de evolução não darwiniana. Por quê?
2. A variabilidade genética é uma medida que reflete a quantidade de variação genética em um determinado grupo de organismos. Se neste grupo existem muitos alelos com freqüência alta, há muita variabilidade genética. Numa população grande que se fragmenta em muitas sub-populações pequenas, o que ocorre, depois de muito tempo na variabilidade genética:
a) em cada uma das subpopulações.
b) na população como um todo
c) justifique.
Projeto 2. Simulação de seleção natural.
A seleção natural é considerada como o único processo modulador da evolução. Ela atua sempre no sentido de levar as populações a um estado de maior adaptabilidade. Dentro dos processos conhecidos que atuam na evolução dos organismos, a seleção natural pode ter tanto a sua intensidade como sua direção estabelecidas. A seleção natural é um processo estatístico, ou seja, ela atua quando existem diferenças de probabilidades de que determinados genótipos ou fenótipos deixem descendência viável. É importante salientar que a intensidade da atuação da seleção natural é relativa, ou seja, um determinado genótipo pode ser bem adaptado com relação a outros genótipos, mas pode não sê-lo se comparado a um genótipo até então não existente.
Um modelo de seleção que pode ser utilizado para uma introdução ao assunto é o elaborado por Sewall Wright e que analisa os efeitos de valores adaptativos (ou coeficientes de seleção) para cada um dos três genótipos de um loco autossômico com dois alelos. Utilize um programa de computador de Gen´´tica de populações para simular a mudança nas freqüências gênicas em vários casos deste modelo.
PROCEDIMENTOS:
O programa precisa dos seguintes dados:
a) a freqüência inicial do alelo A. Comece sempre com um valor alto (ex. 0.9). Isto simularia uma situação na qual este alelo estaria quase monomórfico e o alelo a surgisse por migração. Use também, para cada caso, valores iniciais diferentes.
b) o coeficiente de seleção para cada um dos três genótipos. obs: como se trata de um valor relativo, um dos genótipos deverá apresentar o coeficiente de seleção igual a zero.
c) o número de gerações.
As seguintes situações deverão ser simuladas:
|
situação |
valores adaptativos |
coeficientes de seleção |
classificação (complete) |
|
1 |
w AA = WAa > Waa |
s AA = sAa < saa |
seleção contra homozigotos recessivos |
|
2 |
w AA = WAa < Waa |
s AA = sAa > saa |
|
|
3 |
w AA < WAa = Waa |
s AA > sAa = saa |
|
|
4 |
w AA > WAa = Waa |
s AA < sAa = saa |
|
|
5 |
w AA > WAa > Waa |
s AA < sAa < saa |
seleção contra homozigotos e heterozigotos |
|
6 |
w AA < WAa < Waa |
s AA > sAa > saa |
|
|
7 |
w AA < WAa > Waa |
s AA > sAa < saa |
seleção favorecendo heterozigotos |
|
8 |
w AA > WAa < Waa |
s AA < sAa > saa |
As situações de número 7 e 8 deverão ser repetidas várias vezes com os mesmos valores, modificando-se apenas a freqüência gênica inicial.
Questões:
1. Qual é o comportamento do valor adaptativo médio em todas as situações analisadas? Por quê?
2. Compare todas as situações salientando as diferenças e semelhanças em:
a) Há tendência de extinção de um alelo? Qual?
b) O processo é mais rápido ou mais lento? Atenção: para poder responder esta questão, é importante que se utilize coeficientes de seleção de mesma ordem de magnitude.
c) Há apenas equilíbrio trivial (quando há extinção de um alelo) ou há algum tipo de equilíbrio não trivial (quando os dois alelo se mantêm em certas freqüências)?
