Princípios gerais dos métodos de distância
Duas seqüências macromoleculares podem apresentar
um valor de identidade entre seus monômeros que varia entre 0 (nenhum
dos monômeros é idêntico para cada uma das posições)
até 1 (ou 100%), onde as seqüências são completamente
idênticas. Distâncias são valores que podem ser interpretados
como medidas geométricas entre pontos que são calculadas
a partir da comparação entre as seqüências.
1. Matriz de distâncias
Para um conjunto com N seqüências são possíveis
N*(N-1)/2 distâncias que podem ser representadas por uma matriz triangular
onde a diagonal conteria apenas valores 1 (quando uma seqüência
é comparada com ela mesma):
| |
1
|
2
|
3
|
4
|
...
|
N-1
|
N
|
|
1
|
|
d(1,2)
|
d(1,3)
|
d(1,4)
|
...
|
d(1,N-1)
|
d(1,N)
|
|
2
|
|
|
d(2,3)
|
d(2,4)
|
...
|
d(2,N-1)
|
d(2,N)
|
|
3
|
|
|
|
d(3,4)
|
...
|
d(3,N-1)
|
d(3,N)
|
|
4
|
|
|
|
|
...
|
d(4,N-1)
|
d(4,N)
|
|
...
|
|
|
|
|
|
...
|
...
|
|
N-1
|
|
|
|
|
|
|
d(N-1,N)
|
|
N
|
|
|
|
|
|
|
|
2. Árvores construídas a partir da matrix de distâncias.
Arvores são representações de dimensão
fracionária nas quais cada um dos pontos que representam as seqüências
são ligados a cada um dos outros pontos por um único caminho.
Uma árvore representará a matriz de distâncias se a
soma dos trechos dos caminhos percorridos entre dois pontos for a distância
entre esses pontos de acordo com a matriz.
Por exemplo, considere a seguinte matriz com distâncias arbitrárias
entre os pontos A, B, C, D e E:
| |
A
|
B
|
C
|
D
|
E
|
|
A
|
|
82
|
192
|
192
|
192
|
|
B
|
|
|
192
|
192
|
192
|
|
C
|
|
|
|
58
|
94
|
|
D
|
|
|
|
|
94
|
|
E
|
|
|
|
|
|
Abaixo está um diagrama onde todas as distâncias entre
os pontos estão representadas:

Observação: O diagrama acima, com linhas
retas, tem existência em espaços de N-1 dimensões,
onde N é o número de pontos. No caso acima ele deve ser interpretado
como tetradimensional.
Para as distâncias acima existe uma única
solução de representação de árvore onde
as distâncias acima estão contempladas:
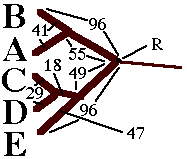
Na árvore acima existe um ponto (R)
que tem a propriedade de ter uma distância igual para todos os pontos
termninais da árvore. Quando existe tal ponto, as distâncias
são ditas "ultramétricas".
Para se chegar na árvore, é empregado
um algoritmo (conjunto de procedimentos automatizados) que é representado
através de uma alegoria aqui.
Considere agora a seguinte matriz de distâncias:
| |
A
|
B
|
C
|
D
|
E
|
|
A
|
|
125
|
163
|
189
|
239
|
|
B
|
|
|
86
|
184
|
234
|
|
C
|
|
|
|
222
|
272
|
|
D
|
|
|
|
|
122
|
|
E
|
|
|
|
|
|
Mais uma vez existe uma única solução
pra uma árvore que contempla as distâncias acima:

Não há, na árvore acima, nenhum
ponto que seja equidistante dos pontos terminais. No entanto, as distâncias
estão perfeitamente contempladas. Nesse caso as distâncias
não são ultramétricas, mas apenas aditivas.
Todas as distâncias ultramétricas são aditivas também,
mas o inverso não pode ser afirmado. A obtenção da
árvore pode ser imaginada através da seguinte alegoria.
3. Algoritmos de construção de árvores a partir de
distâncias.
O primeiro algoritmo desenvolvido para a construção
de árvores a partir da matrizes de distâncias foi o UPGMA.
("Unweighted pair group method using arithmetic averages", Sneath
e Sokal, 1973). Com esse algoritmo é possível apenas a reconstrução
de árvores com distâncias ultramétricas. Mesmo que
essa propriedade não seja verificada na matriz, a árvore
resultante sempre apresenta um ponto equidistante dos terminais.
Devido a essa limitação o emprego desse algoritmo tem
sido criticado.
Existem outors algoritmos que não
exigem a necessidade de ultrametricidade, tais como o de Farris (1970),
de "Neighbor joining" (Saitou e Nei, 1987), etc. Para revisões,
consultar Nei (1987), Swofford et al. (1996) e Russo et al. (2000). De
modo geral, os métodos lidam de modo diferente com os erros, que
consistem na falta da propriedade de aditividade dos dodos de distâncias.
4. Modelos de substituição de nucleotídeos e distâncias.
Em primeiro lugar, é preciso se levar em conta
que, a partir da comparação de seqüências atuais,
não é possível se saber todas as substituições
realmente ocorridas durante a evolução das seqüências
pelo fato de que em uma única posição pode ter havido
mais que uma substituição. Veja a seguinte animação.
Para se lidar com esse problema, é necessário
que as distâncias sejam corrigidas, de acordo com algum modelo. O
mais simples foi desenvolvido por Jukes e Cantor (1969) de acordo com a
premissa que as substituições entre os nucleotídeos
ocorram com igual taxa:

Graficamente, teremos a seguinte relação
entre a proporção de nucleotídeos diferentes e a distância
corrigida:

Existem outros modelos, mais realistas, que levam
em conta o fato de que existe uma fração dos nucleotídeos
que nunca são substituídos, de que as transições
(substituições entre pirimidinas ou entre purinas)
são mais freqüentes que as transições (substituições
de purina para pirimidina ou vice versa), de que as taxas de substituições
entre os sítios são heterogêneas, de que as proporçoes
entre as bases são diferentes, etc. O princípio continua
o mesmo, ou seja, verificamos nas seqüências atuais um número
menor de substituições do que realmente ocorreu na evolução.
Com os modelos pretendemos saber qual é o valor de distância
mais adequado para a reconstrução da árvore.
5. Causas de taxas diferentes em linhagens.
Obviamente, o tempo decorrido entre o ancestral de todos
os organismos e esses é exatamente a mesma, conforme representado
aqui.
Entretanto vários conjuntos de dados mostram que existem taxas de
evolução molecular diferentes para linhagens de organismos
diferentes. Uma das explicações para essas observaçãoes
é de que organismos com tempos de geração diferentes
teriam taxas de evolução molecular diferentes. Nesse caso,
espécies com tempo de geração curto teriam um maior
número de gerações para um determinado intervalo de
tempo absoluto do que espécies de tempo de geração
maior. Existe uma grande dsicussão sobre esse tema que envolve os
seguintes aspectos:
a) Se duas espécies contemporâneas apresentam tempos de
geração diferentes, a espécie ancestral das mesmas
tinha um único tempo de geração e não é
possível, na maioreia das situações, se determinar
o período em que houva a diferenciação quanto a esse
aspecto.
b) Mesmo quando há diferença nos tempos de geração,
pode ser que no nível das gerações celulares de células
germinativas é o mesmo, o que causaria diferenças nas taxas
de mutação.
Além da questão relativa aos tempos
de geração diferentes, existe a questão demográfica.
Espécies que apresentam grandes flutuações populacionais
estão sujeitas a apresentar aumento de variabilidade genética
quando a população cresce em número (conforme visto
no modelo desenvolvido por Kimura e Ohta, em 1974, aqui
representado). Em populações que diminuem de tamanho, é
verificado o efeito contrário, ou seja, diminuição
de variabilidade genética. Espécies que aumentam e diminuem
de tamanho constantemente são encontradas entre as espécies
colonizadoras, reconhecidamente oportunistas. Para tornar o problema ainda
mais complexo, as espécies colonizadoras tendem a ter tempos de
geração mais curtas que as suas espécies próximas
não colonizadoras!
Página principal





