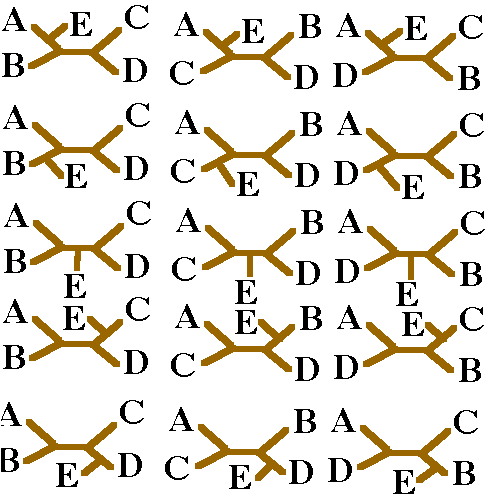Princípios gerais do método de parcimônia

O princípio de parcimônia é um princípio filosófico largamente empregado na Ciência. Foi proposto por um filósofo inglês, Ockam no século XVII e seu enunciado é aproximadamente o seguinte: Se existe mais de uma explicação para uma dada observação, devemos adotar aquela mais simples.
O método de máxima parcimônia foi empregado em análises de seqüências moleculares com o propósito de reconstrução de árvores filogenéticas como uma simplificação do método de máxima verossimilhança por Eck e Dayhoff (1967). Já havia sido empregado implicitamente com o propósito de explicar a origem das inversões aninhadas nos cromossomos politênicos de espécies de Drosophila, em 1936 por Sturtervant e Dobzhansky.

1. O princípio da parcimônia nas reconstruções filogenéticas a partir de dados de seqüências macromoleculares.

A aplicação do princípio de máxima parcimônia nas reconstruções filogenéticas é conceitualmente muito simples: Devemos escolher, dentre as árvores possíveis, aquela com o menor número de substituições que seja compatível com as seqüências observadas. Entretanto, a implementação é complexa, pois o número de árvores possíveis pode atingir valores muito altos.
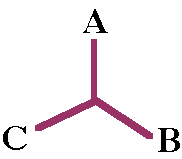
Para 3 seqüências, existe apenas uma árvore possível (que sejam bifurcantes, árvores tais como A--B--C não são consideradas):

Para 4 seqüências, existem 3 árvores (bifurcantes) possíveis.

Para 5 seqüências existem 15 árvores (bifurcantes):

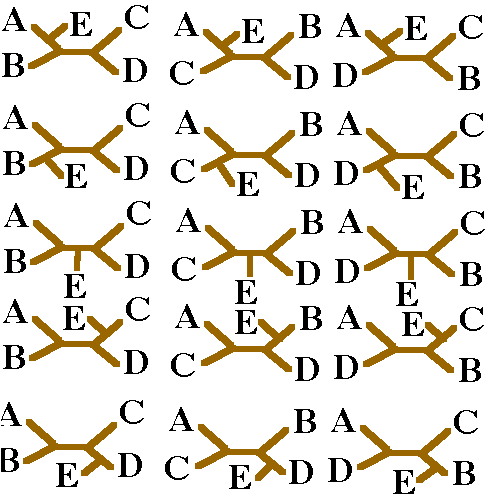O número de árvores cresce muito rapidamente à medida que aumenta o número de seqüências. Você deve ter notado que para saber o número de ávores com N seqüências, multiplica-se o número de árvores com N-1 seqüências pelo número de ramos presentes em uma árvore com N-1 seqüências. Para 10 seqüências,mais de um milhão de árvores são possíveis. Para se atingir o número de partículas elementares do Universo conhecido (~10⁸⁰), bastam 59 seqüências! E isso contando apenas as árvores sem raiz e estritamente bifurcantes.

2. Algoritmos para a reconstrução filogenética com máxima parcimônia.

O algoritmo mais simples de se entender mas que também é o de maior exigência computacional é o de busca exaustiva, onde todas as árvores possíveis são verificadas. Na prática o emprego desse algoritmo é inviável para muitas seqüências. Existe também um algoritmo exato , "branch and bound" (que assegura que a árvore mais parcimoniosa é encontrada), que verifica apenas um subconjunto delas. Existem ainda os algoritmos heurísticos, que, embora não consigam, com certeza, determinar a árvore mais parcimoniosa, analisam um subconjunto muito reduzido das árvores possíveis mas que são mais prováveis de conter a mais parcimoniosa, de acordo com critérios variáveis conforme o algoritmo. Entre este temos o "branch-swaping", o "star decomposition" e o "nearest neighbor interchange".

3. Variações do método de máxima parcimônia.

    O método de parcimônia, em sua forma mais simples, tem como sua principal vantagem, segundo seus defensores, a independência de modelos de evolução. Seus detratores argumentam, no entanto, que na verdade existe um modelo implícito, por exemplo, no qual todos os sítios de uma seqüência macromolecular tiem pesos iguais, de que não é considerada a diferença empírica entre taxas diferentes de transições e transversões, etc, em uma analogia com o modelo de Jukes e Cantor (1969).Certas variantes do método de parcimônia foram propostas para admitir modelos explícitos de evolução. Temos abaixo alguns exemplos:
a) Parcimônia de transversão.
    Nesse método, as mudanças que envolvem transições são simplesmente ignoradas da análise
b) Emprego de uma matriz de passos
    Para contemplar, por exemplo, diferenças entre transições de transversões, são empregadas, a priori, uma contagem diferente para transições e transversões. Por exemplo, com o emprego de uma matriz desse tipo:

DE
PARA		A	T	C	G
	A	-	2	2	1
	T	2	-	1	2
	C	2	1	-	2
	G	1	2	2	-

As transições contam um passo e as transverções contam 2 passos. Uma matriz para seqüências de aminoácidos em proteínas teria a dimensão 20,20.
Outros detalhes poderão ser encontrados em Swofford et al. (1996) e Miyaki et al. (2000).

Página principal