O princípio da MP é que a hipótese mais simples deve ser a escolhida dentre todas as hipóteses possíveis de reconstrução filogenética. Ou seja, a árvore que apresentar o menor número de passos (passos = mudanças de estado de caráter) será a árvore mais parcimoniosa e será a escolhida para explicar um determinado conjunto de dados.

    Existem, no entanto, alguns problemas e limitações. Primeiro, um determinado conjunto de dados pode gerar mais de uma árvore igualmente mais parcimoniosa, pois os dados estudados podem ser acomodados de formas diferentes e apresentar o mesmo número menor de passos.

    Às vezes podem ser duas árvores outras podem ser centenas de árvores igualmente mais parcimoniosas. Nesse caso, deve imperar o bom-senso, poucas árvores igualmente mais parcimoniosas podem ser "transformadas" numa árvore de consenso, a qual representa uma espécie de média entre as árvores mais parcimoniosas obtidas (os programas computacionais fazem isso automaticamente). Por outro lado, quando muitas árvores igualmente mais parcimoniosas são obtidas, pode estar refletindo que haja politomias reais, ou então que aquele conjunto de dados não seja o mais adequado para o estudo filogenético.

    Um outro problema que pode surgir é a ocorrência de homoplasias na árvore mais parcimoniosa obtida.

    A estimativa do índice de consistência (IC) procura avaliar justamente o grau de homoplasias de uma árvore filogenética, isto é, nos casos em que cada mudança de estado de caráter aparece uma única vez na topologia, o IC será igual a 1,0 (ou 100%), significando que provavelmente aquela árvore está isenta de viéses por causa de homoplasias. É comum impor-se um IC mínimo para a confiança em uma dada árvore. Alguns autores mais puristas chegam até a considerar um IC mínimo de 95%, no entanto, em geral um IC maior ou igual a 75% é bem aceito. ICs abaixo desse valor estão indicando que não há uma boa adequação dos dados à topologia da árvore proposta, tornando-a menos confiável.

    Há outros indexadores usados para avaliar a sustentação dos ramos de uma árvore. Os mais amplamente utilizados são o "bootstrap" e o índice de dacaimento ou índice de Bremer.

    Os índices de "bootstrap" são verificados através da análise de reamostragem de caracteres da matriz de dados, gerando novas matrizes. Em outras palavras, o "bootstrap" essencialmente é uma simulação do que aconteceria se os caracteres fossem sujeitos a receber pesos ou serem revisados. Se, na reamostragem de caracteres, determinados ramos permanecem sempre juntos nas novas topologias simuladas, aquele nó que os une receberá um valor de 100% na árvore original mais parcimoniosa.

    O índice de Bremer ou de decaimento avalia o número de passos necessários que devem ser inseridos em um ramo para que esse sofra colapso (perca a resolução, gerando uma politomia). Dessa maneira, quanto maior o valor do índice de Bremer para um dado ramo, tanto mais esse se encontra sustentado (ou estável) na topologia proposta.

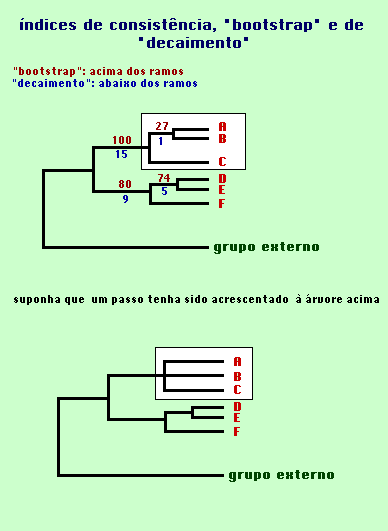
    No exemplo hipotético da figura acima, embora a topologia de árvore possa apresentar um IC razoável, o ramo que origina as linhagens A e B é frágil, bastando um passo a mais para que as linhagens A, B e C colapsem gerando uma politomia. Observe que os valores de "bootstrap" e de decaimento são coerentes entre si.
 
    Existem vários métodos baseados no princípio da MP, como a "parcimônia de Fitch & Wagner", a "parcimônia de Dollo", a "parcimônia de Camin-Sokal". Todos eles baseiam-se em um critério de otimização específico, mas, no entanto, não utilizam modelos evolutivos de substituição de nucleotídeos explícitos.

    Existe muita controvérsia com relação à MP por esta metodologia não se basear em modelo algum. Será isso uma vantagem ou uma desvantagem?

    Independentemente se vantajoso ou não, o fato é que de alguma maneira as metodologias de MP envolvem suposições e a violação das mesmas pode acarretar problemas de interpretação dos dados. A dificuldade, porém, está em se saber quais são essas suposições. Por outro lado, existem outras metodologias que se baseiam em suposições explícitas e essas suposições são modelos claros e objetivos de mudanças evolutivas envolvendo substituição de nucleotídeos. As metodologias que se baseiam em modelos evolutivos são conhecidas como métodos de máxima verossimilhança.
voltar ao começo
voltar à página principal